Searching Algorithms :
A search algorithm is an algorithm for finding an item with specified properties among a collection of items.
It can be used for :
Database/Files.
Data structures
Graphs
String matching
Information retrieval
Elements of a search space defined by a mathematical formula or procedure(roots of equation etc.)
Pseudo Code of Recursive Binary Search :
int binary_search(int A[], int key, int imin, int imax)
{
// test if array is empty
if (imax < imin):
// set is empty, so return value showing not found
return KEY_NOT_FOUND;
else {
// calculate midpoint to cut set in half
int imid = midpoint(imin, imax);
// three-way comparison
if (A[imid] > key)
// key is in lower subset
return binary_search(A, key, imin, imid-1);
else if (A[imid] < key)
// key is in upper subset
return binary_search(A, key, imid+1, imax);
else // key has been found
return imid;
}
}
Improvement in Binary Search Algorithm :
Binary Search takes three paths based on the key comparison:
1)one path for less than
2)one path for greater than
3)one path for equality.
The path for equality is taken only when the record is finally matched, so it is rarely taken. Therefore it can be moved outside the search loop in the deferred test for equality version of the algorithm.
Deferred detection of equality :
int binary_search(int A[], int key, int imin, int imax)
{
// continually narrow search until just one element remains
while (imin < imax) {
int imid = midpoint(imin, imax);
// code must guarantee the interval is reduced at each iteration
assert(imid < imax);
// note: 0 <= imin < imax implies imid will always be less than imax
// reduce the search
if (A[imid] < key)
imin = imid + 1;
else imax = imid;
} // At exit of while:
// if A[] is empty, then imax < imin
// otherwise imax == imin
// deferred test for equality
if ((imax == imin) && (A[imin] == key))
return imin;
else return KEY_NOT_FOUND;
}
How do we search in Dictionary/Telephone Booklet ?
To search on Dictionary/Telephone Booklet , we do Interpolation/extrapolation search.
Interpolation/extrapolation search :
public int interpolationSearch(int[] sortedArray, int toFind)
{
// Returns index of toFind in sortedArray, or -1 if not found
int low = 0;
int high = sortedArray.length – 1,mid;
while (sortedArray[low] <= toFind && sortedArray[high] >= toFind)
{
mid = low + ((toFind - sortedArray[low]) * (high - low)) / (sortedArray[high] - sortedArray[low]);
//out of range is possible here
if (sortedArray[mid] < toFind) low = mid + 1;
else if (sortedArray[mid] > toFind)
// Repetition of the comparison code is forced by syntax limitations.
high = mid - 1;
else return mid;
}
if (sortedArray[low] == toFind)
return low;
else return -1; // Not found
}
Knuth have provided the Proof of above equation : mid = low + ((toFind - sortedArray[low]) * (high - low)) / (sortedArray[high] - sortedArray[low].
Improve Selection Sort : To improve the selection sort, we use Bingo Sort. In this we skip the comparison of same elements.
bingo(array A)
{ This procedure sorts in ascending order. }
begin max := length(A)-1;
{ The first iteration is written to look very similar to the subsequent ones, but without swaps}.
nextValue := A[max];
for i := max - 1 downto 0 do
if A[i] > nextValue then
nextValue := A[i];
while (max > 0) and (A[max] = nextValue) do
max := max - 1;
while max > 0 do begin
value := nextValue;
nextValue := A[max];
for i := max - 1 downto 0 do
if A[i] = value then begin
swap(A[i], A[max]);
max := max - 1;
end else if A[i] > nextValue then
nextValue := A[i];
while (max > 0) and (A[max] = nextValue) do
max := max - 1;
end;
end;
Improvement in Bubble Sort : Stop at the sorting process at that iteration where swapping b/w numbers didn't occur.
Pseudo Code of Bubble Sort Improvement :
procedure bubbleSort( A : list of sortable items )
repeat
swapped = false
for i = 1 to length(A) - 1 inclusive do:
/* if this pair is out of order */
if A[i-1] > A[i] then
/* swap them and remember something changed */
swap( A[i-1], A[i] )
swapped = true
end if
end for
until not swapped
end procedure
Improvement in Insertion Sort :Insertion sort can be improve by using binary search in insertion sort at the time of searching the location of swap element.
That's variant of insertion sort also called as Binary Insertion Sort.
BinaryInsertionSort (int a[], int n)
{
int ins, i, j,tmp;
for (i = 1; i < n; i++)
{
ins = BinarySearch (a, 0, i, a[i]);
if (ins < i)
{
tmp = a[i];
for (j = i - 1; j >= ins; j--)
a[j + 1] = a[j];
a[ins] = tmp;
}
}
}
Comparison of Selection Sort, Bubble Sort and Insertion Sort
Where should we use Insertion Sort instead of Selection Sort and Bubble Sort? :
Where the data set have most of the elements are sorted order. Then we should use insertion sort.
Where should we use Selection Sort or Bubble instead of Insertion sort ?
Where the space requirement is less like as embedded programming, there we should use selection sort/bubble sort. Because in that shifting of element doesn't occur like as insertion sort.
Quicksort is a divide and conquer algorithm :
Steps are:
Step 1 : Pick an element, called a pivot, from the list.
Step 2 : Reorder the list so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
Step 3 : Recursively sort the sub-list of lesser elements and the sub-list of greater elements.
Lets take the example of Quick Sort
Repeat above 4 steps till then small_index cross the big index.
A single quicksort call involves O(n) work plus two recursive calls on lists of size n/2, so the recurrence relation is :T(n) = O(n) + 2T(n/2)
The master theorem tells us that T(n) = O(nlogn)
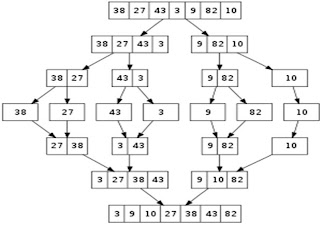
Merge Sort :
Conceptually, a merge sort works as follows :
Step 1: Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
Step 2: Repeatedly merge sublists to produce new sublists until there is only 1 sublist remaining. This will be the sorted list
If the running time of merge sort for a list of length n is T(n), then the recurrence T(n) = 2T(n/2) + n follows from the definition of the algorithm (apply the algorithm to two lists of half the size of the original list, and add the n steps taken to merge the resulting two lists).
The closed form follows from the master theorem T(n) = O(n) + 2T(n/2)
The master theorem tells us that T(n) = O(nlogn)
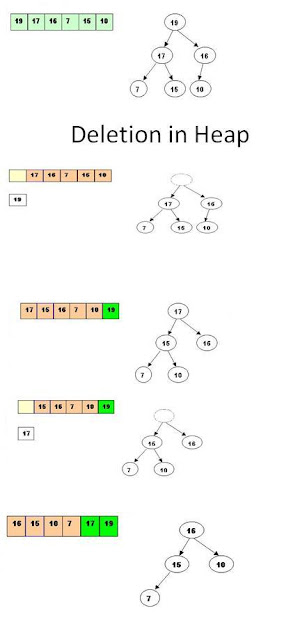
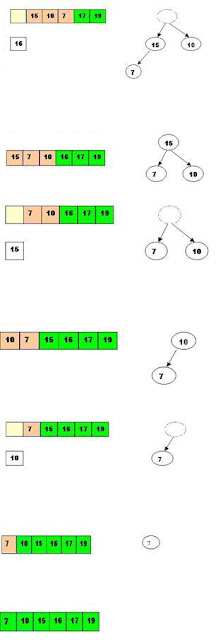
Heap Sort :
Steps are :
Step 1 : Consider the values of the elements as priorities and build the heap tree.
Step 2 : Start deleteMin operations, storing each deleted element at the end of the heap array.
Heap Construction and Deletion :
Comparison Tips :
Quicksort is typically somewhat faster due to better cache behavior and other factors, but the worst-case running time for quicksort is O(n2), which is unacceptable for large data.
Merge sort requires auxiliary space according to value of n, but heapsort requires only a constant amount.
Heapsort is not a stable sort; merge sort is stable.
Merge sort parallelizes well and can achieve close to linear speedup with a trivial implementation; heapsort is not an obvious candidate for a parallel algorithm.
Merge sort is used in external sorting; heapsort is not. Locality of reference is the issue.
Radix Sort :
Steps are :
Step 1 : Take the least significant digit (or group of bits, both being examples of radices) of each key.
Step 2 : Group the keys based on that digit, but otherwise keep the original order of keys. (This is what makes the LSD radix sort a stable sort).
Repeat the grouping process with each more significant digit.
The sort in step 2 is usually done using bucket sort or counting sort, which are efficient in this case since there are usually only a small number of digits.
Example :
Original, unsorted list: 170, 45, 75, 90, 802, 24, 2, 66
Sorting by least significant digit (1s place) gives:
170, 90, 802, 2, 24, 45, 75, 66
[*Notice that we keep 802 before 2, because 802 occurred before 2 in the original list, and similarly for pairs 170 & 90 and 45 & 75.]
Sorting by next digit (10s place) gives:
802, 2, 24, 45, 66, 170, 75, 90
[*Notice that 802 again comes before 2 as 802 comes before 2 in the previous list.]
Sorting by most significant digit (100s place) gives:
2, 24, 45, 66, 75, 90, 170, 802
Radix sort takes O(k*n) time
Shell Sort :
Shellsort is a multi-pass algorithm. Each pass is an insertion sort of the sequences consisting of every h-th element for a fixed gap h (also known as the increment). This is referred to as h-sorting.
An example run of Shellsort with gaps 5, 3 and 1 is shown below :
Generally Gap Sequence is
It needs relatively short code and does not use the call stack. Therefore it use in embedded systems instead of quick sort.