First time when we used the Algorithm ? :
Isn’t when we started to visualize the things?
Isn’t when we started to speak?
Isn’t when we started to identify the words?
Isn’t when we started to learn rules for Addition , Multiplication etc?
Is algorithm related to only computer science?
Mathematics in Algorithms :
Mathematical analysis of algorithms occupies a central position in computer science; reasoning about algorithms independently of the specific devices on which they run can yield insight into general design principles and fundamental constraints on computation.
Mathematics is the core part of Algorithms.
Such as in statistics / probability (i.e. for scientific and financial programming), abstract algebra and number theory (i.e. for cryptography).
The triple of real numbers d1x=(x2-x1), d1y=(y2-y1), d1z=(z2-z1) are called the Cartesian components of displacement vector d1.
Vector Addition is shown below :
Vector Product : Product of two vector computed as :
It also called as scalar product or dot product.
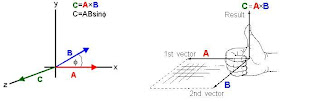
Cross Product of Vector: Vector cross product is computed as :
It also called as Cross Product.
Matrix :
Basic matrix operations are :
Matrix multiplication use at so many places in m/c learning. Time Complexity of matrix multiplication is O(n3). In matrix multiplication .multiplication of each row with each column takes O(n2) and combining them takes O(n). Thats why matrix multiplication takes O(n3) time.
Strassen build algorithm with some equation through which matrix multiplication takes O(n2.807) time.
Cosine Similarity use in m/c learning to find the how much two documents are similar. In below figure cosine similarity is calculated in b/w two documents x and y as :
Eigen Vectors also use in many placed in m/c learning. It use in PCA(Principal Component Analysis) for dimension reduction regarding m/c learning. It also use for reducing term-document matrix dimension in IR(Information Retrieval).
An Eigen vector of a square matrix is a non-zero vector that, when multiplied by the matrix, yields a vector that is parallel to the original.
Right eigenvector : Av = λv
Left eigenvector : vA = λv
Eigen vector present by graph and matrix shown below :
Eigen vector example shown below :
In above example first is eignen vector because here Ax = λx but in second Ax != λx so second is not an eigen vector.
Eigen value calculation for eigen vector as :
From above example eigne value calculated are 3 and 4. Lets calculate eigen vector from eigen value 3 in below example as :
Probability :
Some of Common Usage in Computer Science are :
Artificial intelligence(Bayesian Sequence Prediction)
Machine learning(Naive Bayes Classifier)
Game Theory(Strategy, Decision Making)
Difference b/w mutually exclusive and independent probability is mutually exclusive happens on same experiment and independent happens on different experiment. Ex. Tossing a coin once and getting head or tail is mutually exclusive. But if tossing a coin twice and getting HH or TT is independent Probability.
Bayesian Probability :
Bayes Theorem Application : Naive Bayes Classifier
Isn’t when we started to visualize the things?
Isn’t when we started to speak?
Isn’t when we started to identify the words?
Isn’t when we started to learn rules for Addition , Multiplication etc?
Is algorithm related to only computer science?
Mathematics in Algorithms :
Mathematical analysis of algorithms occupies a central position in computer science; reasoning about algorithms independently of the specific devices on which they run can yield insight into general design principles and fundamental constraints on computation.
Mathematics is the core part of Algorithms.
Such as in statistics / probability (i.e. for scientific and financial programming), abstract algebra and number theory (i.e. for cryptography).
Recently Google Published Mathematics at Google
Vectors and Matrix :
Vectors Application:
Machine learning, a supervised learning method used for classification.(Feature Vector)
Cryptography(Initialization vector (IV))
Vector graphics (VML : XML for to produce vector graphics)
Matrix Application :
Eigen Vector
Linear Equations
Vectors :
Vectors quantities are physical quantities that have both magnitude and direction
The displacement vector shown below :
The triple of real numbers d1x=(x2-x1), d1y=(y2-y1), d1z=(z2-z1) are called the Cartesian components of displacement vector d1.
Vector Addition is shown below :
Vector Product : Product of two vector computed as :
It also called as scalar product or dot product.
Cross Product of Vector: Vector cross product is computed as :
It also called as Cross Product.
Matrix :
Basic matrix operations are :
Matrix multiplication use at so many places in m/c learning. Time Complexity of matrix multiplication is O(n3). In matrix multiplication .multiplication of each row with each column takes O(n2) and combining them takes O(n). Thats why matrix multiplication takes O(n3) time.
Strassen build algorithm with some equation through which matrix multiplication takes O(n2.807) time.
Cosine Similarity use in m/c learning to find the how much two documents are similar. In below figure cosine similarity is calculated in b/w two documents x and y as :
Eigen Vectors also use in many placed in m/c learning. It use in PCA(Principal Component Analysis) for dimension reduction regarding m/c learning. It also use for reducing term-document matrix dimension in IR(Information Retrieval).
An Eigen vector of a square matrix is a non-zero vector that, when multiplied by the matrix, yields a vector that is parallel to the original.
Right eigenvector : Av = λv
Left eigenvector : vA = λv
Eigen vector example shown below :
In above example first is eignen vector because here Ax = λx but in second Ax != λx so second is not an eigen vector.
Eigen value calculation for eigen vector as :
From above example eigne value calculated are 3 and 4. Lets calculate eigen vector from eigen value 3 in below example as :
Probability :
Some of Common Usage in Computer Science are :
Artificial intelligence(Bayesian Sequence Prediction)
Machine learning(Naive Bayes Classifier)
Game Theory(Strategy, Decision Making)
Some Basic Probabilities are :
Difference b/w mutually exclusive and independent probability is mutually exclusive happens on same experiment and independent happens on different experiment. Ex. Tossing a coin once and getting head or tail is mutually exclusive. But if tossing a coin twice and getting HH or TT is independent Probability.
Conditional Probability :
Conditional probability is the probability that an event will occur, when another event is known to occur or to have occurred. If the events are A and B respectively, this is said to be "the probability of A given B". It is commonly denoted by P(A|B).
Bayesian Probability :
Bayes' theorem (alternatively Bayes' law or Bayes' rule) is a theorem with two distinct interpretations :
1) In the Bayesian interpretation, it expresses how a subjective degree of belief should rationally change to account for evidence.
2) In the frequentist interpretation, it relates inverse representations of the probabilities concerning two events.
Bayesian interpretation : Bayes' theorem then links the degree of belief in a proposition before and after accounting for evidence.
For example, somebody proposes that a biased coin is twice as likely to land heads than tails. Degree of belief of in this might initially be 50%. The coin is then flipped a number of times to collect evidence. Belief may rise to 70% if the evidence supports the proposition.
For proposition A and evidence B
P(A): the prior, is the initial degree of belief in A.
P(B): the posterior, is the degree of belief having accounted for B.
P(B|A)/P(B) : represents the support B provides for A.
Frequentist interpretation : In this probability measures a proportion of outcomes. Bayes' theorem under this interpretation is most easily visualized using tree diagrams.
Bayes Theorem Application : Naive Bayes Classifier
A naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong (naive) independence assumptions
Set Theory :
Some of Common Usage in Computer Science are :
Graph Theory(MST, Shortest Path)
Game Theory(set of players, set of moves)
Artificial Intelligence(Fuzzy Set)
Some of basic operations in set theory are :
Set Theory :
Some of Common Usage in Computer Science are :
Graph Theory(MST, Shortest Path)
Game Theory(set of players, set of moves)
Artificial Intelligence(Fuzzy Set)
Some of basic operations in set theory are :
Union
Intersection
Set difference : {2,3,4} \ {1,2,3} -> {4}
Symmetric difference : {1,2,3} and {2,3,4} -> {1,4}
Cartesian product
Power set
Relationships between Sets
Equality : {1, 2, 3} = {3, 2, 1} = {1, 1, 2, 3, 2, 2}
Subsets : A ⊆ B and A ⊂ B
Disjoint : A = {even numbers} and B = {1, 3, 5, 11, 19}, then A and B are disjoint.
Venn Diagram
Truth Table
Fuzzy Set : Fuzzy set is the set where crisp boundary doesn't exist b/w set. Below the example of fuzzy set :














No comments:
Post a Comment